The Fundamentals of Options

Everything you have to know

The stock market offers countless ways to grow your wealth. Most investors are familiar with the basic concept: buy low, sell high. But what if you could profit from falling prices? Or limit your downside while maintaining unlimited upside? Enter options, financial instruments that have been around for centuries yet remain mysterious to many investors. You've probably heard of them, maybe even considered using them, but found yourself overwhelmed by complex terminology and mathematics. In this article, we'll strip away the complexity and build a solid understanding of how options work. After all, you wouldn't drive a car without understanding how the gas and brake pedals work, the same principle applies to options and all other financial products. Let's dive into the fundamentals of options that every investor should know.

What is an option?

Imagine you're planning a vacation for next summer. You find the perfect hotel, but you're not completely sure about your travel dates yet. The hotel offers you two choices: book a non-refundable room for $800, or pay a $50 deposit now to reserve the right to book the room at $800 until three months before your intended stay. If your plans change, you lose only the $50 deposit instead of the full $800. If you decided to buy this, this is actually an option that the hotel sold to you, let me explain further.

In financial markets, options work the same way but instead of hotel rooms, we're dealing with stocks. Just like you bought the right to book a room, you can buy the right to purchase (or sell) shares of a company at a specific price in the future. When you want the right to buy shares, it's called a call option. When you want the right to sell shares, it's called a put option. The price at which you can buy or sell the shares is called the strike price, similar to the $800 room rate in our hotel example. If Apple is trading at $180 and you have a call option with a strike price of $170, your option is in the money because you can buy shares below the market price. If the strike price was $190 instead, your option would be out of the money since buying at $190 when the market price is $180 wouldn't make sense. Most stock options are "American-style," meaning you can exercise your right any time before expiration. Some options, particularly index options, are "European-style," which means you can only exercise them on the expiration date itself.

The payoff of options

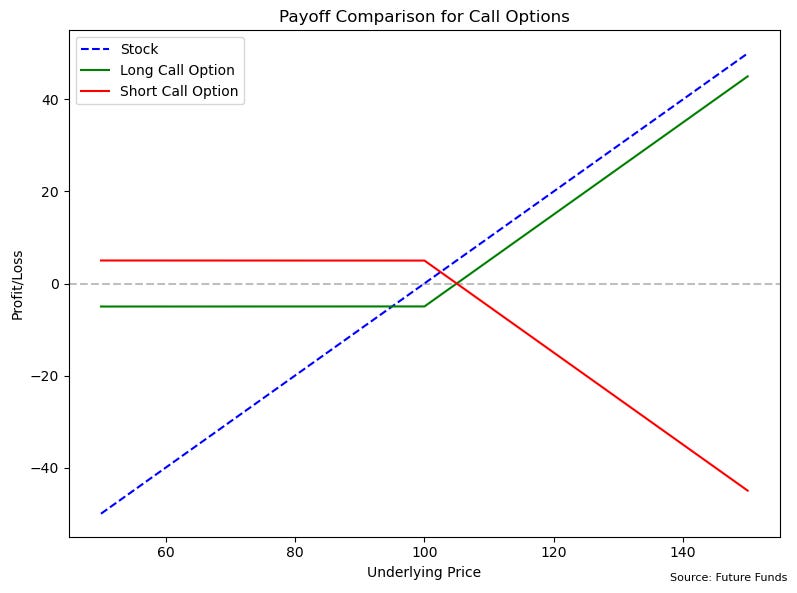
Figure 1

Looking at Figure 1, we see three different investment choices at the date of expiration: simply owning a stock (blue dashed line), buying a call option (green line), and selling a call option (red line). Each starts with the stock at $100, and we'll use this as our strike price. The option premium, which is the upfront cost you pay to buy an option or receive when selling an option, is $5. This premium is why the green line (buying a call) starts at -$5 (you paid $5 upfront) and the red line (selling a call) starts at +$5 (you received $5 upfront).

When you buy a stock, it's straightforward: the stock goes up $1, you make $1; it goes down $1, you lose $1. But options give us more interesting possibilities because of this upfront premium payment.

When you buy a call option (green line), you're paying $5 for the right to buy at $100 on some specific time in the future. Think of it as insurance, your maximum loss is just the $5 premium, even if the stock crashes. Once the stock rises above $100, each dollar increase adds to your profit. Break even happens at $105 (covering your $5 premium), and beyond that, your profits soar just like owning the stock, but with far less money at risk.

Selling a call option (red line) puts you in the insurance company's shoes. You collect the $5 premium upfront, that's your maximum profit. But if the stock rises above $100, you start losing money, potentially without limit. This mirrors the buyer's position exactly, where they gain, you lose.

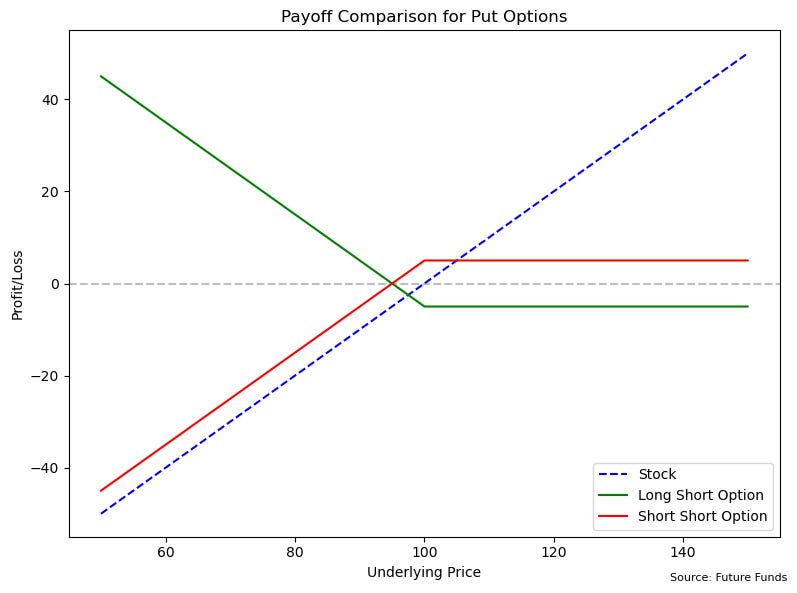
Figure 2

Put options work like calls but for falling prices seen in Figure 2. Think of buying a put (green line) as insurance against price drops, you profit when the stock falls below the strike price, while your risk is capped at the premium paid. Every dollar decrease becomes profit, just like the call option worked for increases. Over time, both calls and puts lose value as expiration approaches, we call this time decay.

Selling puts (red line) again mirrors the buyer's position. You collect a premium now but promise to buy if prices fall. Just as the call seller faces unlimited risk on the upside, put sellers face significant risk on the downside.

This mirror-image relationship between buyers and sellers is fundamental to options, each gain has a corresponding loss, each limited risk has a matching unlimited risk. It's a perfect balance, like a seesaw. When you limit your risk by buying options, someone else is accepting that risk. When you collect a premium by selling options, you're taking on risk that someone else wants to avoid.

Pricing of options

The payoff diagrams show us what options are worth at expiration, but determining their fair price before then is where the real artistry begins. Over the years, financial minds have developed two elegant approaches to solve this puzzle: the Black-Scholes model and the binomial tree model. Let's start with the more intuitive one.

Imagine you're playing chess. To win, you must think several moves ahead, considering each possible move your opponent might make. Option pricing works remarkably similarly, we map out all possible future prices and work backward to find today's value. This is the essence of the binomial tree model.

Figure 3

Let's walk through a real example using Figure 3. Our stock starts at $100, and at each 6-month step (making this a one-year option), it can move up or down by 15%. These movements are typically based on the stock's historical behavior, more volatile stocks have bigger potential moves, but we'll keep it simple. Like a chess game unfolding, we first map out all possible paths over the year: up-up reaching $132.25, up-down or down-up landing at $97.75, or down-down falling to $72.25.

Now comes the clever part. At the one-year expiration, calculating the option's value becomes simple, it's the stock price minus our $95 strike price (or zero if we're below the strike). This gives us our endpoint values: $37.25 when the stock reaches $132.25, $2.75 at $97.75, and $0 at $72.25.

To work backwards through each 6-month period, we use what's called risk-neutral probability, a mathematical tool that helps us value options as if everyone were indifferent to risk. Our formula looks like this:

Option Value = (1/1+r₆ₘ) × [p × (up value) + (1-p) × (down value)]

Here, 'r₆ₘ' is our 6-month interest rate (half of the 5% annual rate) to adjust for the time value of money, and 'p' is our special risk-neutral probability that makes the math work. For the left middle node at 6 months, we calculate $22.35 using its one-year values of $37.25 and $2.75. The right node at 6 months gives us $1.57 from its possible one-year values of $2.75 and $0. One final step back brings us to the current fair value today: $13.37. This is what a rational investor should pay for this option today.

The Black-Scholes model, which revolutionized options trading in 1973, follows the same logic but uses calculus to handle infinite price movements. Think of it as a super-powered binomial model that can process countless price paths simultaneously. It made options trading practical by providing instant prices, though it only works for European-style options. The binomial approach, while simpler, handles both European and American options with equal grace.

The beauty in both approaches lies in their core principle: the future is uncertain, but if we can map out its possibilities and work backwards with the right mathematics, we can find fair value today. What seems like complex financial wizardry is really just systematic thinking about future possibilities, something we naturally do every time we plan ahead or make a strategic decision.

This pricing dance between present and future, between certainty and possibility, is what makes options fascinating. We've transformed uncertainty into a precise number using nothing but logical thinking and mathematics.

Why should you care?

Remember the hotel booking example we started with? Chances are you've already traded options without even realizing it. That "flexible" booking rate? An option. The ability to cancel your flight for a small fee? Another option. Even that extended warranty you considered for your new phone follows the same principles we just explored.

While we've unraveled some of the mystery behind options, we've only scratched the surface. We haven't delved into what makes option prices move day to day, or why some options are more expensive than others. But next time you hear terms like "call option" or "strike price," you'll understand the fundamentals of what's being discussed. What seemed like complex financial wizardry at first is, at its core, just a sophisticated way of buying the right to make decisions later, something we all do in our daily lives.

Just like our binomial tree showed us, the power of options lies in their flexibility and the possibilities they create. Whether you're planning to trade them or just want to understand the financial world better, you now have the foundation to appreciate these fascinating financial instruments.

Thank you for your attention, let me know in the comments what you thought of the article, I read all the comments with interest